넘을 수 없는 물리적 장벽 : 메모리 vs. 디스크

메모리 접근: 나노초 (ns)

> 100,000배 차이

디스크 접근: 밀리초 (ms)

데이터베이스의 인덱스는 대부분 디스크(HDD/SSD)에 저장됩니다. 디스크 접근(I/O)은 메모리 접근보다 수만 배는 느리기 때문에, CPU가 아무리 빨라도 디스크에서 데이터를 읽어오는 시간이 전체 성능을 좌우합니다.

⇒ 목표 : 그래서 우리는 디스크에 접근하는 횟수를 어떻게든 최소화해야합니다.

후보1 : 이론상 가장 빠른 해시인덱스

hash-index-disadvantage

해시자료구조는 특정 값을 찾는 동등비교(=)연산에서 O(1)의 속도를 보장하기 때문에 이론상 가장 빠릅니다.

그러나, 데이터가 정렬되어 있지 않아 범위검색(<, >, BETWEEN)이 불가능합니다. 따라서 범용적인 DB 인덱스로는 한계가 명확합니다.

후보2 : 그렇다면 정렬된 구조인 BST(이진탐색트리)는?

bst-disadvantage

그렇다면 정렬된 구조인 이진탐색트리는 어떨까요?

왼쪽 서브트리 : 루트보다 작은 값
오른쪽 서브트리 : 루트보다 큰 값

이 구조덕분에 데이터 탐색과 범위 검색이 모두 가능합니다.

그러나, 데이터가 정렬된 순서로 입력되면 트리가 한쪽으로 치우칩니다. 균형이 깨진 트리는 사실상 연결리스트(Linked List)와 같아져 조회 성능이 최악의 경우 O(n)으로 저하됩니다. 이러한 특성때문에 DB 인덱스로 사용하기엔 리스크가 큽니다.

후보3: 스스로 균형을 잡는 트리 AVL은 어때? (레드블랙트리)

avl-disadvantage

균형이진트리는 데이터 삽입/삭제시 스스로 구조를 재조정하여 항상 균형을 유지합니다. 따라서 BST의 최악의 경우인 O(n)을 방지하고, 어떤 상황에서도 O(log n)의 조회 성능을 보장합니다.

하지만 균형이 잡혀도 자식노드가 2개뿐인 이진트리는 데이터 양이 많아질수록 필연적으로 트리의 높이가 매우 깊어집니다.

트리의 높이 = 조회 작업에 필요한 최대 디스크 I/O 횟수

수억 개의 데이터가 있다면, 트리의 높이는 수십 레벨에 달할 수 있고, 이는 곧 수십 번의 디스크 접근을 의미합니다. 여전히 너무 느립니다.

B-Tree : 높이 대신 너비를 택하다

btree_vs_binary_tree_height_width

B-Tree란 하나의 노드에 여러 개의 키를 저장하는 다진 트리입니다.(Multi-way Tree)

하나의 노드에 많은 데이터를 담기 때문에 트리의 높이를 극적으로 낮춥니다. 따라서 수억 개의 데이터도 단 3~4 레벨의 높이로 표현할 수 있으므로, 몇 번의 디스크 I/O만으로 조회 작업을 완료할 수 있습니다.

또, DB는 데이터를 페이지 또는 블록 단위로 읽어옵니다. B-Tree 노드 크기를 이 “페이지” 단위에 맞추면, 한번의 디스크 I/O로 노드의 여러 키 값을 가져올 수 있습니다. 이는 캐시 적중률을 높이고 조회 성능을 극대화합니다.

모든 노드가 데이터를 갖는다

btree_internal_and_leaf_node_data_storage

키(Key)와 해당 데이터(Data)가 모든 노드(루트,브랜치,리프)에 저장될 수 있습니다. 따라서 리프 노드까지 가지 않아도, 운좋으면 중간 노드에서 조회 작업이 끝날 수 있습니다. 그러나 이것이 항상 장점은 아닙니다.

B+Tree : B-Tree의 단점 보완한 구조

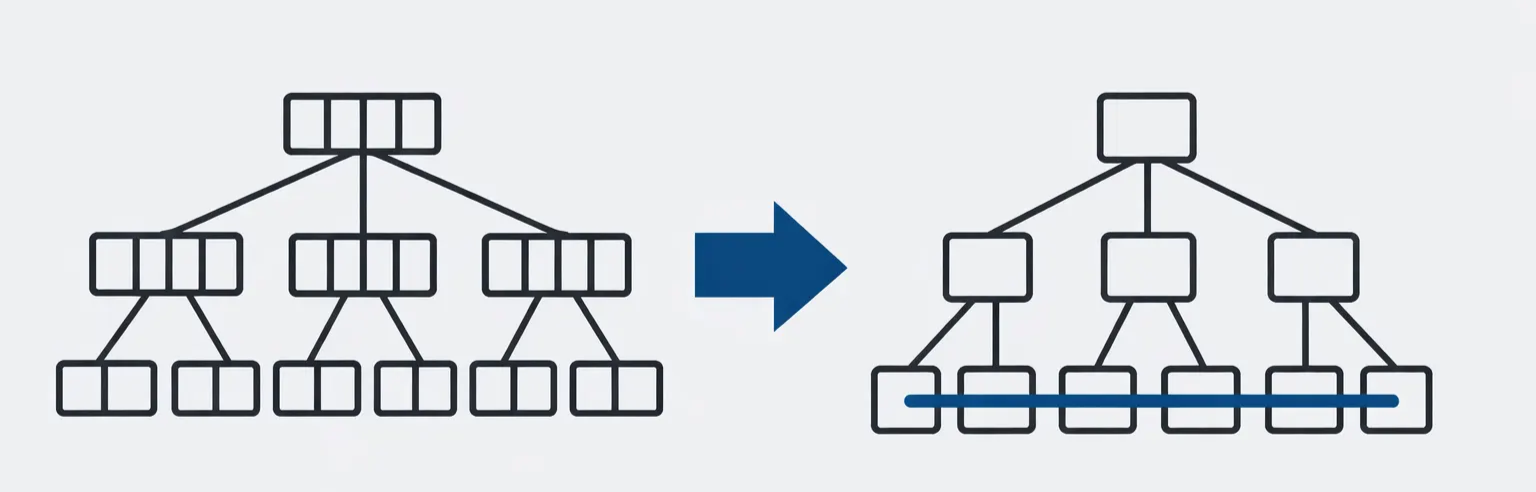
btree_to_bplustree_leaf_linking

B+Tree는 B-Tree의 장점을 계승하고, DB 환경에서 최적화된 개선을 가진 자료구조입니다.

데이터는 오직 리프 노드에만 저장한다. 브랜치 노드는 경로탐색을 위한 인덱스 역할로만 수행한다.
모든 리프 노드가 연결리스트(Linked List)로 연결되어있다.

1) 리프노드에만 저장, 브랜치 노드는 인덱스로만 → 너비는 더 넓고 높이는 더 낮게!

btree_vs_bplustree_internal_node_structure

브랜치 노드에 데이터를 저장하지 않으니, 동일한 노드 크기(페이지 크기)에 더 많은 키(경로 정보)를 저장할 수 있습니다.

따라서 노드가 더 많이 분기해서 트리의 너비는 넓어지고, 높이는 더 낮아집니다. 이는 디스크 I/O 횟수가 더 줄어들 수 있음을 의미합니다.

2) 리프 노드 연결리스트로 순차 스캔 → 범위 검색 성능 UP!

btree_range_query_traversal

모든 리프 노드들이 포인터로 서로 연결된 Linked List 구조를 가집니다. 이 구조 덕분에 B-Tree처럼 트리를 다시 올라가지 않고, 리프노드만 순차적으로 탐색하면 되므로, 훨씬 범위 탐색과 정렬 성능이 극대화됩니다.

ex. WHERE age BETWEEN 25 AND 50

범위의 시작 값(25)를 찾아 리프노드로 이동한다. (B-Tree)
트리를 다시 탐색하지 않고 연결된 리프노드를 따라 순차적으로 스캔한다(→30→45→50)

거의 모든 현대 DBMS 표준 : MySQL InnoDB 엔진 예시

mysql-innodb-dbms-structure

프라이머리 인덱스(클러스터형 인덱스) : 리프노드에 실제 데이터 레코드 전체가 저장됩니다.
세컨더리 인덱스(보조 인덱스) : 리프노드에는 데이터 주소 대신 레코드의 PK 값이 저장됩니다. 따라서 세컨더리 인덱스로 조회하면, 먼저 PK 값을 찾은 후, 이 PK 값으로 프라이머리 인덱스를 한번 더 조회해야 실제 데이터에 접근할 수 있습니다.

마무리

[문제] 느린
디스크 I/O

→

해시 인덱스 범위 검색
불가능

→

BST 불균형 시
O(N) 위험

→

균형 트리 높은 트리
I/O 부담

→

B-Tree 낮은 높이
I/O 최소화

→

B+Tree 범위 검색
최적화

DB 인덱스의 자료구조는 “어떻게 디스크 접근을 최소화 할 것인가”에 대한 답을 찾아온 과정이었습니다.

B+Tree는 다음과 같은 특징으로 이 문제에 대한 최적의 답을 제시합니다.

낮고 넓은 트리 : 최소한의 디스크 I/O로 조회성능 높임
리프 노드 연결 : 압도적인 범위 검색 성능
구조적 일관성 : BST와 달리, 예측 가능하고 안정적인 성능

DB 인덱스 성능의 핵심은 알고리즘이 아니라 디스크 I/O입니다.

이것이 MySQL, PostgreSQL, Oracle 등 대부분의 현대 DBMS가 B+Tree를 표준으로 채택한 이유입니다.

[DB] 인덱스 자료구조로 B-Tree(혹은 B+Tree)를 사용하는 이유